报告题目（1）：Multiple solutions for elliptic equations with quasilinear perturbation

报告时间：2020 12月14日上午9点-10点。

报告地点：腾讯会议， ID：590 303 852， 会议密码：123456

报告人：刘祥清（云南师范大学）

报告摘要：In this talk, we study elliptic equations with quasilinear perturbation and obtain multipllicity result by elliptic regularization method.

报告题目（2）：Nodal solutions for Kirchhoff equation in 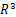with critical growth

报告时间：2020 14月12日上午10点-11点。

报告地点：腾讯会议， ID：590 303 852， 会议密码：123456

报告人：刘祥清（云南师范大学）

报告摘要：In this talk, we consider the Kirchhoff equation in 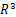  with critical growth. We assume that the potential function V is a radial function and is bounded from below by a positive constant. We prove the problem has a radial solution, having k nodal domains exactly.

报告题目（3）：Localized nodal solutions for quasilinear Schr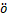dinger equations  

报告时间：2020 12月14日上午11点-12点。

报告地点：腾讯会议， ID：590 303 852， 会议密码：123456

报告人：刘祥清（云南师范大学）

报告摘要：In this talk, we study the existence of localized nodal solutions for a class of semiclassical quasilinear Schrodinger equations including, as a special case, the Modified Nonlinear Schr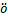dinger Equation(MNLS) . We establish for small  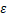the existence of a sequence of localized nodal solutions concentrating near a given local minimum point of the potential function, by developing new variational perturbation method to treat this class of non-smooth variational problems. The new method allows the perturbed variational functionals share critical points with the original functional. This method allows us to avoid any limiting process from the perturbed problems to the original problem, and it is effective in dealing with multiple existence of solutions.

邀请人：周育英